Hướng dẫn chi tiết cách xác định tâm đường tròn ngoại tiếp tam giác cân

Trong hình học phẳng, việc xác định tâm đường tròn ngoại tiếp tam giác cân là một bài toán cơ bản nhưng quan trọng. Hôm nay, vesinhantoanthucpham.com.vn sẽ hướng dẫn chi tiết cách xác định tâm đường tròn ngoại tiếp tam giác cân, từ lý thuyết cơ bản đến các phương pháp thực hành.

Kiến thức cơ bản về tam giác cân

Định nghĩa tam giác cân

Tam giác cân là tam giác có hai cạnh bằng nhau. Các tính chất quan trọng của tam giác cân bao gồm:

• Hai cạnh bằng nhau
• Hai góc đáy bằng nhau
• Có một trục đối xứng
• Đường cao từ đỉnh trùng với đường phân giác và trung tuyến

Các yếu tố đặc biệt

1. Đường cao
2. Đường trung tuyến
3. Đường phân giác
4. Đường trung trực

Đường tròn ngoại tiếp tam giác

Định nghĩa đường tròn ngoại tiếp

Đường tròn ngoại tiếp tam giác là đường tròn đi qua cả ba đỉnh của tam giác. Tâm của đường tròn này là giao điểm của ba đường trung trực của tam giác.

Tính chất đặc biệt

1. Tâm đường tròn ngoại tiếp nằm trên trục đối xứng của tam giác cân
2. Khoảng cách từ tâm đến ba đỉnh tam giác bằng nhau
3. Bán kính đường tròn ngoại tiếp là khoảng cách từ tâm đến bất kỳ đỉnh nào

Xem thêm Tìm hiểu chi tiết về bài tập cấp số cộng và các phương pháp giải

Phương pháp xác định tâm đường tròn ngoại tiếp

Phương pháp 1: Sử dụng đường trung trực

Các bước thực hiện:

1. Vẽ đường trung trực của hai cạnh bất kỳ
2. Tìm giao điểm của hai đường trung trực
3. Giao điểm chính là tâm đường tròn ngoại tiếp

Chú ý: Trong tam giác cân, chỉ cần vẽ đường trung trực của đáy và một cạnh bên.

Phương pháp 2: Sử dụng tính chất đối xứng

Các bước thực hiện:

1. Xác định trục đối xứng của tam giác cân
2. Vẽ đường trung trực của đáy
3. Giao điểm của hai đường này chính là tâm đường tròn ngoại tiếp

Công thức tính toán liên quan

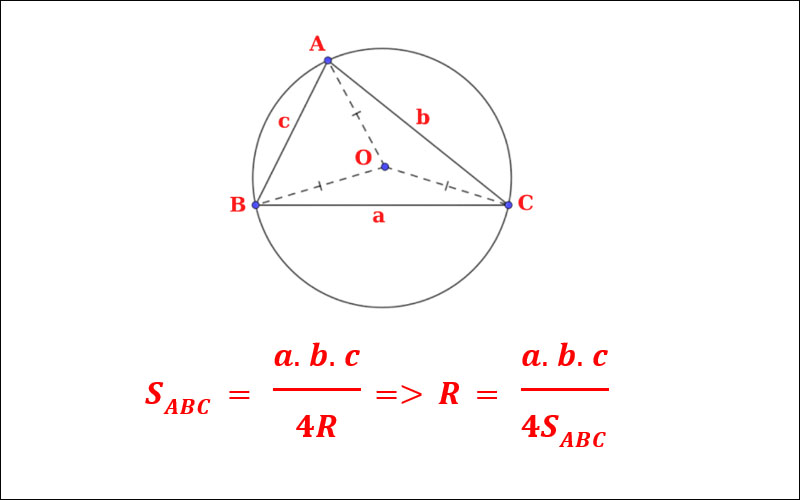
Công thức tính bán kính

R = abc/(4S) Trong đó:

• R: bán kính đường tròn ngoại tiếp
• a, b, c: độ dài các cạnh tam giác
• S: diện tích tam giác

Công thức đặc biệt cho tam giác cân

Khi tam giác cân có:

• Hai cạnh bằng nhau a
• Đáy là b
• Chiều cao là h

Thì bán kính đường tròn ngoại tiếp là:

R = a²/(4h)

Các bài toán thực hành

Bài toán mẫu 1

Đề bài: Cho tam giác cân ABC có AB = AC = 5cm, BC = 6cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Lời giải:

1. Tính chiều cao của tam giác: h = √(a² - (b/2)²) h = √(25 - 9) h = 4cm
2. Áp dụng công thức: R = 25/(4×4) = 1.5625cm

Bài toán mẫu 2

(Tiếp tục với các bài toán mẫu khác…)

Các lỗi thường gặp và cách khắc phục

Lỗi về vẽ hình

1. Không đảm bảo hai cạnh bằng nhau
2. Vẽ đường trung trực không chính xác
3. Xác định sai trục đối xứng

Lỗi về tính toán

1. Áp dụng sai công thức
2. Nhầm lẫn đơn vị đo
3. Sai số trong quá trình tính toán

Xem thêm Hướng Dẫn Chi Tiết Cách Giải Phương Trình Sin x = 0: Từ Cơ Bản Đến Nâng Cao

Ứng dụng thực tiễn

Trong thiết kế và xây dựng

1. Thiết kế mái vòm
2. Xây dựng cấu trúc đối xứng
3. Tính toán khoảng cách đều

Trong nghệ thuật và kiến trúc

1. Thiết kế logo
2. Trang trí nội thất
3. Quy hoạch không gian

Phương pháp kiểm tra kết quả

Kiểm tra bằng đo đạc

1. Đo khoảng cách từ tâm đến ba đỉnh
2. Kiểm tra tính vuông góc của đường trung trực
3. Xác nhận vị trí trên trục đối xứng

Kiểm tra bằng tính toán

1. Áp dụng định lý Pitago
2. Kiểm tra tỷ lệ các đoạn
3. Xác nhận các góc bằng nhau

Kết luận

Việc xác định tâm đường tròn ngoại tiếp tam giác cân là một kỹ năng quan trọng trong hình học. Thông qua việc nắm vững các phương pháp và công thức, chúng ta có thể giải quyết nhiều bài toán phức tạp liên quan đến hình học phẳng. Hy vọng những chia sẻ từ vesinhantoanthucpham.com.vn sẽ giúp các bạn hiểu rõ hơn về chủ đề này.

Thông tin liên hệ:
Email: [email protected]
Website: vesinhantoanthucpham.com.vn