Thông Tin Chi Tiết Về Cách Tính Bán Kính Đường Tròn Ngoại Tiếp Tam Giác Đều

Trong lĩnh vực an toàn thực phẩm, việc hiểu và áp dụng các công thức toán học, đặc biệt là hình học, có vai trò quan trọng trong thiết kế bao bì, tối ưu hóa không gian lưu trữ và bố trí thiết bị. Hôm nay, chúng ta sẽ tìm hiểu chi tiết về cách tính bán kính đường tròn ngoại tiếp tam giác đều.
Cơ Sở Lý Thuyết Về Đường Tròn Ngoại Tiếp
Định Nghĩa và Đặc Điểm
- Đường tròn ngoại tiếp tam giác là đường tròn đi qua cả ba đỉnh của tam giác
- Tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực của tam giác
- Với tam giác đều, tâm đường tròn ngoại tiếp trùng với trọng tâm và tâm đường tròn nội tiếp

Các Yếu Tố Cơ Bản
- Bán kính đường tròn ngoại tiếp (R)
- Cạnh tam giác đều (a)
- Đường cao (h)
- Diện tích tam giác (S)
Công Thức Tính Bán Kính Đường Tròn Ngoại Tiếp
Công Thức Cơ Bản
- Từ độ dài cạnh:
- R = a/(√3) Trong đó:
- R: bán kính đường tròn ngoại tiếp
- a: độ dài cạnh tam giác đều
- Từ diện tích:
- R = (2S)/(3×(√3)) Trong đó:
- S: diện tích tam giác đều
Công Thức Mở Rộng
- Từ đường cao:
- R = (2h)/3 Trong đó:
- h: đường cao tam giác đều
- Từ bán kính đường tròn nội tiếp:
- R = 2r Trong đó:
- r: bán kính đường tròn nội tiếp
Ứng Dụng Trong Thiết Kế và Sản Xuất
Thiết Kế Bao Bì
- Tối ưu hóa không gian:
- Tính toán diện tích bao bì tối thiểu
- Thiết kế hình dạng sản phẩm hiệu quả
- Giảm lãng phí nguyên liệu
- Bố trí sản phẩm:
- Sắp xếp các sản phẩm hình trụ
- Tối ưu hóa không gian lưu trữ
- Thiết kế kệ trưng bày

Thiết Kế Thiết Bị
- Bồn chứa hình trụ:
- Tính toán dung tích tối ưu
- Thiết kế đáy bồn chứa
- Bố trí hệ thống ống dẫn
- Hệ thống làm mát:
- Thiết kế quạt thông gió
- Bố trí ống dẫn khí
- Tối ưu hóa luồng không khí
Xem thêm Thông Tin Chi Tiết Về Toán GMAT Trong Ngành Vệ Sinh An Toàn Thực Phẩm
Phương Pháp Tính Toán Chi Tiết
Các Bước Tính Toán
- Xác định dữ liệu đã biết:
- Độ dài cạnh hoặc
- Diện tích tam giác hoặc
- Đường cao
- Áp dụng công thức phù hợp:
- Chọn công thức dựa trên dữ liệu có sẵn
- Thực hiện tính toán
- Kiểm tra kết quả
Ví Dụ Minh Họa
- Ví dụ 1:
- Cho tam giác đều cạnh 6cm
- R = 6/(√3) ≈ 3.46cm
- Ví dụ 2:
- Cho diện tích tam giác đều 36cm²
- R = (2×36)/(3×√3) ≈ 13.86cm
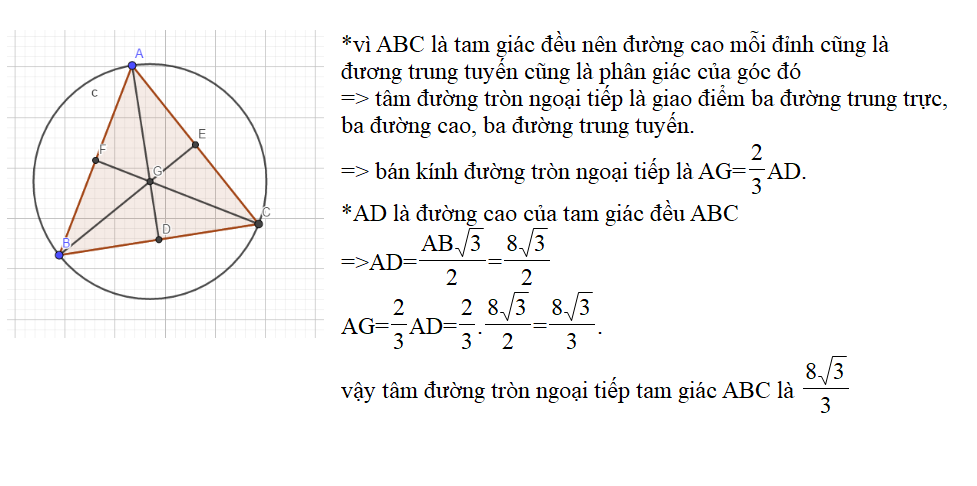
Kiểm Tra và Xác Minh Kết Quả
Phương Pháp Kiểm Tra
- Kiểm tra bằng công thức khác:
- Sử dụng các công thức tương đương
- So sánh kết quả
- Kiểm tra bằng đồ họa:
- Vẽ hình để kiểm chứng
- Đo đạc trực tiếp
Các Lỗi Thường Gặp
- Sai số trong tính toán:
- Làm tròn số không phù hợp
- Nhầm đơn vị đo
- Nhầm lẫn công thức:
- Sử dụng sai công thức
- Áp dụng không đúng trường hợp
Xem thêm Thông Tin Chi Tiết Về Công Thức Logarit Đầy Đủ: Hướng Dẫn Toàn Diện
Ứng Dụng Thực Tế
Trong Công Nghiệp Thực Phẩm
- Thiết kế bồn trộn:
- Tính toán kích thước tối ưu
- Bố trí cánh khuấy
- Thiết kế hệ thống làm mát
- Hệ thống đóng gói:
- Thiết kế máy đóng gói tự động
- Bố trí băng chuyền
- Tối ưu hóa quy trình

Trong Bảo Quản Thực Phẩm
- Thiết kế kho lạnh:
- Bố trí không gian lưu trữ
- Tối ưu hóa luồng không khí
- Thiết kế hệ thống làm lạnh
- Bố trí thiết bị:
- Sắp xếp máy móc hiệu quả
- Tối ưu hóa không gian làm việc
- Đảm bảo an toàn vệ sinh
Kết Luận và Tổng Kết
Việc hiểu và áp dụng đúng cách tính bán kính đường tròn ngoại tiếp tam giác đều không chỉ quan trọng trong toán học mà còn có nhiều ứng dụng thực tế trong ngành công nghiệp thực phẩm. Từ thiết kế bao bì đến bố trí thiết bị, những kiến thức này giúp tối ưu hóa quy trình sản xuất và đảm bảo an toàn vệ sinh thực phẩm.
Để biết thêm thông tin chi tiết về các ứng dụng toán học trong an toàn thực phẩm, vui lòng truy cập website vesinhantoanthucpham.com.vn hoặc liên hệ qua email [email protected].
Bài viết được cung cấp bởi Kiến Thức Vệ Sinh An Toàn Thực Phẩm – vesinhantoanthucpham.com.vn
Thông tin liên hệ:
- Email: [email protected]
- Website: vesinhantoanthucpham.com.vn


